Oggi facciamo un post più teorico, che prescinde dall’uso di uno specifico software.
Può esserti capitato di sentir parlare di centroidi e di creazione di centroidi da poligoni o di trasformazione di poligoni in centroidi.
Si ma…cos’è un centroide? ‘na cosa che se magna? 😀
Seguici e ti spiegheremo subito cosa sono.
Per prima cosa dobbiamo partire dalla definizione di poligono: un poligono, nella geometria piana Euclidea, è una qualunque figura geometrica delimitata da una linea spezzata chiusa. I vari segmenti che formano la linea in questione vengono definiti lati, mentre i punti in comune sono definiti vertici.
I poligoni sono classificati in:
- poligoni semplici: figure i cui lati non si intersecano;
- poligoni complessi: figure i cui lati si intersecano (aggiungiamo che raramente vengono usati nel GIS, anzi spesso sono segnale di un errore topologico – ma questo è un altro post)
Ancora, i poligoni semplici sono classificati in:
- poligoni convessi: sono caratterizzati dal non contenere i prolungamenti dei propri lati (a) o anche dal fatto che se scegliamo due qualsiasi punti interni al poligono, il segmento che ha per estremi tali punti è sempre contenuto nel poligono stesso (b);
- poligoni concavi: un poligono concavo contiene almeno uno dei prolungamenti dei suoi lati (c) e, inoltre, sarà sempre possibile individuare due punti interni ad esso il cui segmento non è contenuto interamente al suo interno (d).

Ma perché parliamo di poligoni se l’argomento del post sono i centroidi? Perché un centroide è il baricentro geometrico di un poligono.
Il baricentro geometrico di un insieme di punti è il punto le cui coordinate, in un dato riferimento cartesiano, sono il risultato della media aritmetica delle rispettive coordinate dei punti. Ora, dato che un poligono altro non è che un insieme di punti, avremo che il suo centroide è proprio il baricentro geometrico.
I centroidi nei diversi tipi di poligoni
Il baricentro di un poligono, cioè il nostro centroide, assume una posizione diversa a seconda della tipologia di poligono considerato:
- nel caso di poligoni convessi, il centroide ricade all’interno del loro contorno. Pensa, ad esempio a rettangolo, rombo, quadrato, ecc… (fig. sotto)
- nel caso di poligoni concavi, il centroide può ricadere anche esternamente ad essi, come ad esempio per la figura piana falce di luna. Per cui, se quando proverai a creare dei centroidi, qualcuno uscirà fuori dal poligono di partenza, potrebbe essere normale (ovviamente dovrai verificare che il poligono di partenza sia concavo)
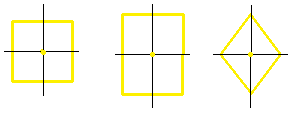
Esistono anche poligoni composti, in cui il calcolo del baricentro geometrico richiede dei concetti matematici un pò più avanzati legati al concetto di momento statico (ma anche questo è un altro post). Per fortuna i nostri software GIS fanno tutto il lavoro per noi!
Bene, questo post è finito. Se ti è piaciuto condividilo! Hai dubbi o suggerimenti? Lascia pure un commento.
Puoi vedere questi concetti applicati nella pratica guardando i video (qui e qui), sul nostro canale YouTube (iscriviti!!!), e leggendo i post (qui e qui).
Ci GISsiamo al prossimo post!
Ciaooo