La pendenza in QGIS. La guida definitiva.

Ciao a tutti. Oggi ti facciamo vedere come calcolare la pendenza con QGIS, approfondendo le diverse opzioni che il software implementa nella tool apposita.

1. La tool pendenza

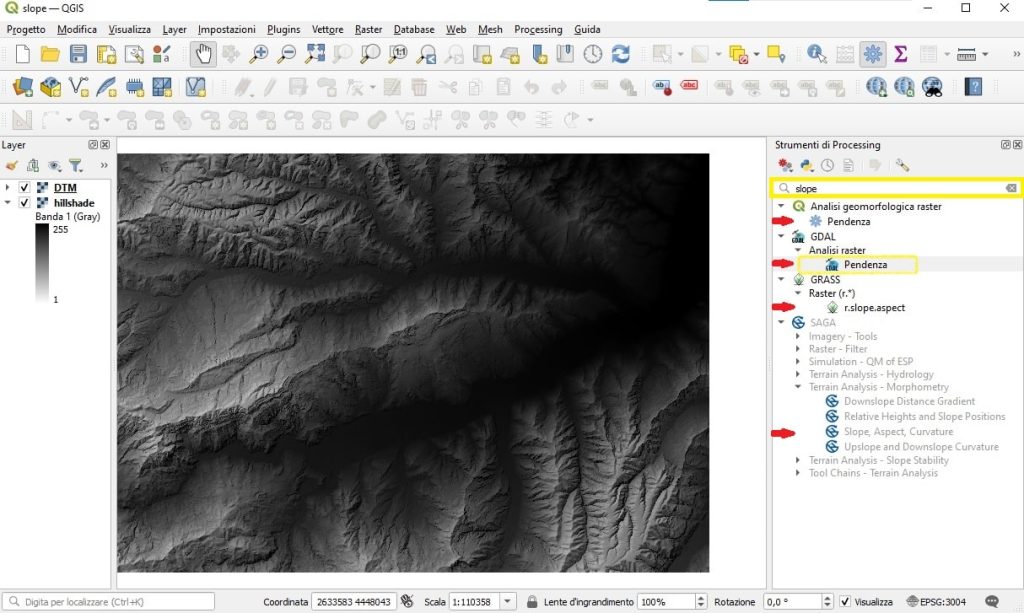
In QGIS sono presenti diverse tool per il calcolo della pendenza. Se andiamo nel pannello degli strumenti di processing e scriviamo slope, cioè la parola inglese per la pendenza, ci appariranno tutte. Abbiamo scritto slope piuttosto che pendenza perché alcune librerie non hanno una traduzione in italiano e quindi scrivendo pendenza avremmo trovato meno tool.

Dopo aver inserito la nostra parola chiave vediamo che c’è una tool Pendenza tra gli strumenti propri di QGIS, una nella libreria GDAL, una tra gli strumenti di GRASS e una tra gli strumenti di SAGA.

Ciascuna di esse consente di attivare opzioni diverse nel calcolo della pendenza e alcune permettono di effettuare altri tipi di Terrain Analysis.

La tool che vedremo oggi è quella di GDAL, Pendenza appunto, che si trova nel gruppo di strumenti Analisi raster. Puoiaccedervi anche andando nel menu Raster: nella sezione Analisi troverai proprio la tool Pendenza di GDAL.

2. Impostiamo input e output della tool Pendenza

Partiamo dall’impostare gli elementi più semplici nella tool pendenza: l’input e l’output.

Come input abbiamo preparato un DTM con risoluzione di 5m derivante da rilievo LiDAR. Lo selezioniamo come Layer in ingresso. Si tratta di un file monobanda, quindi nella casella Numero banda non dobbiamo fare nulla.

Saltiamo direttamente al file di output nella sezione Pendenza e diciamo a QGIS dove e come salvare il raster di output che produrremo.

Possiamo passare a vedere l’impostazione degli altri parametri.

3. Pendenza espressa in percentuale invece che in gradi

Per capire se mettere o meno la spunta alla casella Pendenza espressa in percentuale invece che in gradi, vediamo la definizione matematica di pendenza.

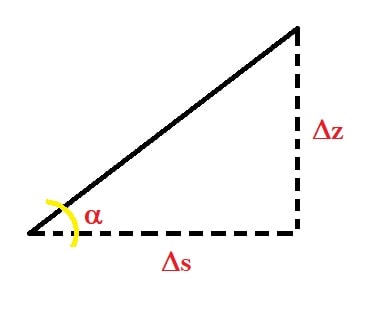
La pendenza, trigonometricamente, è la tangente dell’angolo formata da una linea inclinata e, per un segmento discreto, è definita come il rapporto tra la variazione di quota Δz e lo scostamento lungo il quale si ha tale variazione di quota Δs.

Quindi la pendenza è questa:

 tan (α) = Δz / Δs.

Tuttavia nella pratica lavorativa, ma anche quotidiana, pensa ad esempio alla segnaletica stradale, la pendenza può essere espressa in due modi.

1. Il primo modo: la pendenza, cioè il valore di tan (α), viene moltiplicata per 100. In questo modo la pendenza viene espressa come percentuale. Tuttavia, pur essendo una percentuale, non aspettarti che il valore massimo sia 100, che infatti corrisponde solo ad una inclinazione di 45°. Se, ad esempio, temporaneamente, non consideriamo gli altri parametri della tool pendenza e la eseguiamo, vediamo che il valore massimo stimato è molto superiore a 100. Questo perché la tangente di un angolo può variare da 0 (per un angolo di 0°) ad infinito (per un angolo di 90°). Sicuramente, in natura, valori così alti di pendenza sono possibili e corrisponderanno a variazioni di quota brusca (il geologo del team mi suggerisce che questa situazione implica un gradiente di rilievo elevato).

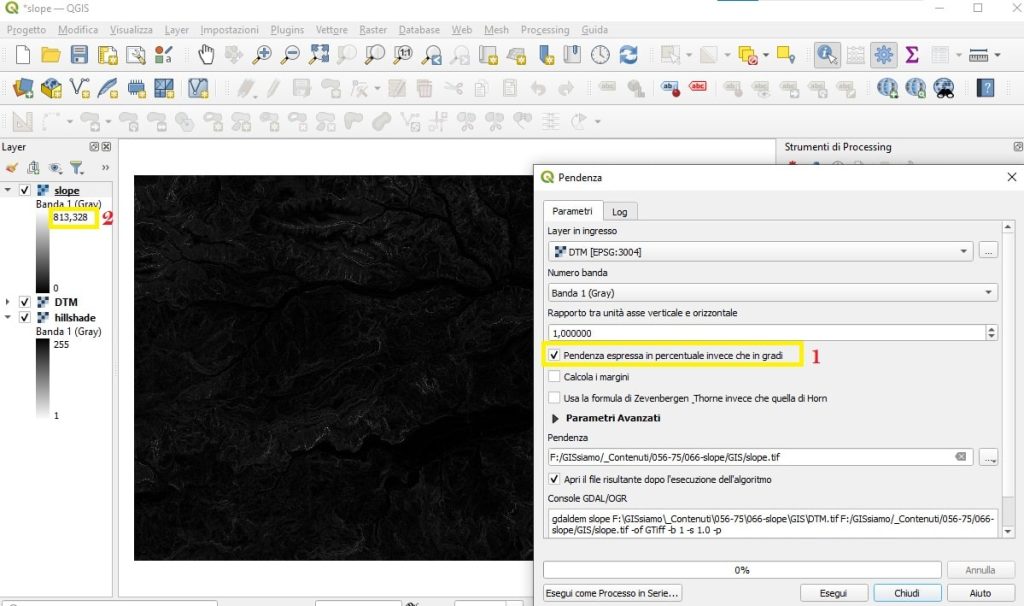
2. Il secondo modo: si esegue l’arcotangente di α,in modo da ricavare l’angolo α di inclinazione. Quindi, con questo modo la pendenza viene identificata con l’inclinazione e varierà in un range da 0 a 90 gradi.

QGIS di default calcola la pendenza con questo secondo metodo, come inclinazione espressa in gradi. Ma se mettiamo la spunta alla voce Pendenza espressa in percentuale invece che in gradi potremo anche calcolarla con il primo metodo e cioè in percentuale.

4. Rapporto tra unità asse verticale e orizzontale

Adesso che sai che la pendenza è il rapporto tra variazione di quota sull’unità di lunghezza, possiamo vedere cosa inserire nell’opzione Rapporto tra unità asse verticale e orizzontale.

Questa opzione, presente anche in altri strumenti di QGIS, sia rappresentativi che analitici, può servire a due scopi:

1. Omogeneizzare le unità di misura di quota e lunghezza. Se l’unità di misura di queste due grandezze è diversa, in questa casella può essere inserito il fattore di conversione tra le due, ottenuto proprio dividendo l’unità di misura usata per le quote per l’unità di misura usata per le lunghezze. Nel nostro caso il Sistema di Riferimento è proiettato ed è in metri. Le quote sono anche riportate in metri, dunque possiamo lasciare 1.
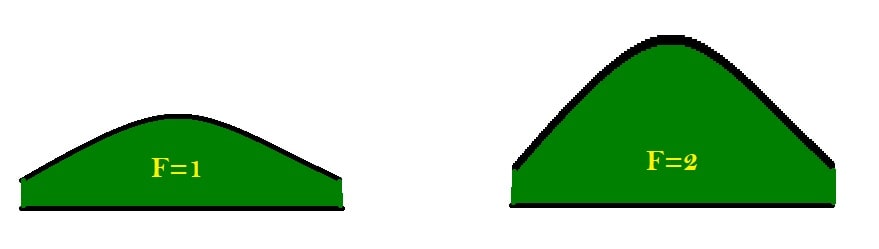
2. Enfatizzare le variazioni di quota. Questo può essere utile, a volte, quando ad esempio l’area studiata è piuttosto omogenea dal punto di vista delle pendenze, per cui abbiamo bisogno di enfatizzare i valori per valutare meglio le piccole variazioni.

Certamente questa opzione va usata con consapevolezza e moderazione.

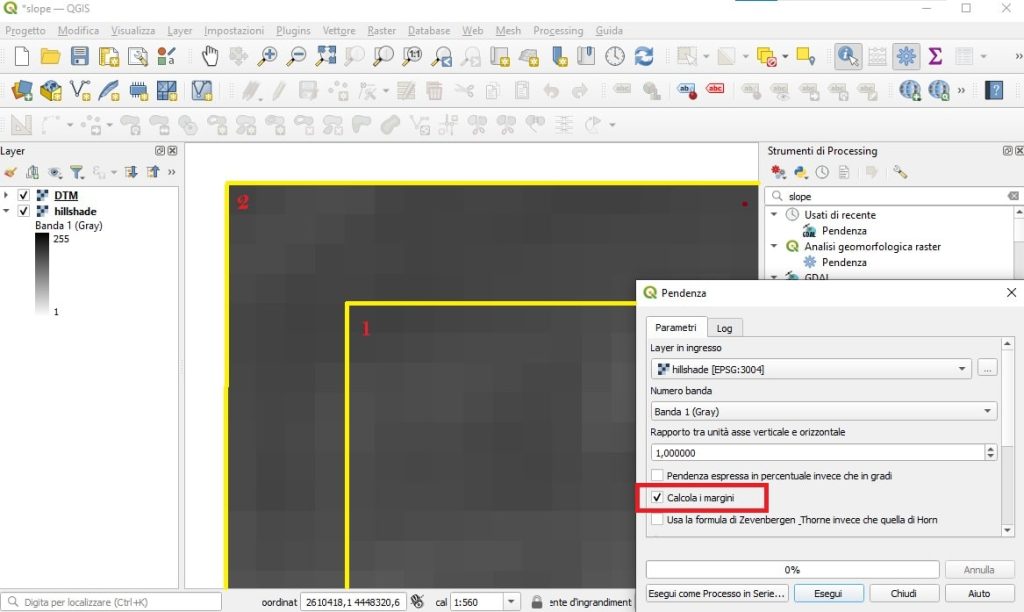
5. Calcola i margini

Per capire l’opzione Calcola i margini dobbiamo ricordare cosa sono gli effetti di bordo nell’analisi raster

Immaginiamo di guardare un pixel al centro di un raster (1). Intorno a lui ci sono tanti pixel utili a calcolare la pendenza.

Guardiamo invece un pixel che si trova nello spigolo in alto a sinistra dello stesso raster (2). Ha a disposizione un numero molto minore di pixel per eseguire lo stesso calcolo. Lo stesso vale non solo per questo pixel, ma per tutti quelli che si trovano lungo il margine del raster. Gli errori di calcolo derivanti dalla mancanza di sufficienti informazioni nell’intorno dei pixel di margine di un raster vengono chiamati effetti di bordo.

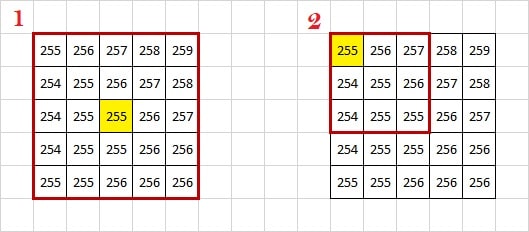
La soluzione a questo problema è avere a disposizione un DTM un po’ più grande dell’area di studio (1), in modo che, mettendo la spunta all’opzione Calcola i margini, non ci saranno problemi lungo i bordi.

Invece, se il DTM coincide esattamente con l’area di cui vuoi calcolare la pendenza (2), allora bisogna disattivare l’opzione Calcola i margini. Altrimenti il NoData intorno al DTM verrebbe considerato come una quota uguale a 0 e inserito nel calcolo delle pendenze. Invece, non mettendo la spunta su questa opzione, verranno considerati nel calcolo solo i pixel che effettivamente hanno il valore di quota. Certo, così il problema dell’effetto di bordo non si risolve, ma quantomeno non vengono calcolati finti gradienti di rilievo elevati o bruschi salti di quota che non rispecchiano la vera morfologia dell’area studiata.

6. Usa la formula di Zevenbergen-Thorne invece che quella di Horn.

La definizione trigonometrica della pendenza è estremamente chiara per uno spazio monodimensionale. Ma in uno spazio bidimensionale modellato da un raster il calcolo si complica un po’, anche se noi cercheremo di semplificare il più possibile i concetti.

Intanto la pendenza è dotata di una direzione. Immagina di inclinare il pixel che rappresenta una porzione discreta di un versante: ci sono tantissimi modi in cui questo può essere inclinato.

Per questo motivo si usa l’operatore gradiente: si tratta di un operatore che viene applicato su una quantità scalare, in questo caso la variazione di quota, e restituisce un vettore, dotato di intensità, direzione e verso. Nel caso di un versante l’intensità del vettore è costituita dal valore di massima pendenza mentre la direzione di massima pendenza può essere calcolata ugualmente tramite l’esposizione, su cui pure sicuramente faremo un post.

Il gradiente si applica calcolando le derivate parziali sulla quota. Anche in questo caso, se il procedimento teorico è chiaro, nella pratica applicata su un raster non lo è altrettanto, perché è vero che il DTM modella una variabile continua, ma lo fa discretizzandola nei quadretti che costituiscono un raster.

Per questo motivo esistono diverse formule per il calcolo della pendenza.

Due delle formule più usate in letterature sono proprio quelle citate nella tool Pendenza di QGIS: la formula di Horn e la formula di Zevenbergen-Thorne.

Noi qui non entriamo nel merito delle formule, ma vi lasciamo qualche riferimento da leggere, per chi volesse approfondire, alla fine di questo post.

Vi diciamo però, semplificando e sintetizzando, quando è meglio usare l’una piuttosto che l’altra.

• La formula di Horn, usata di default dal software, restituisce un effetto più smussato. Per questo motivo è più adatto a DTM che, essendo stati interpolati (ad esempio quando li deriviamo dalle curve di livello), contengono più rumore. Sempre a causa di questo maggiore livello di smoothing la formula di Horn è più adatta a studi di tipo più generico, magari allo scopo di studiare il paesaggio o analisi morfologiche.
• La formula di Zevenbergen-Thorne, invece, restituisce un risultato più dettagliato e meno uniformizzato. Di conseguenza si può applicare con buoni risultati per i DTM derivanti, ad esempio, da volo LiDAR. Inoltre, restituendo una slope più di dettaglio è una formula da usare se il calcolo della pendenza serve per effettuare analisi morfometriche di dettaglio in cui essa è usata come parametro.

A questo punto sai tutto sulla tool Pendenza di QGIS. Non ci resta che calcolarla.

I parametri che noi usiamo sono quelli di default di QGIS, quindi:

• Rapporto tra unità asse verticale e orizzontale uguale a 1;
• Pendenza espressa in gradi;
• Non calcoliamo i margini
• Facciamo usare a QGIS la formula di Horn

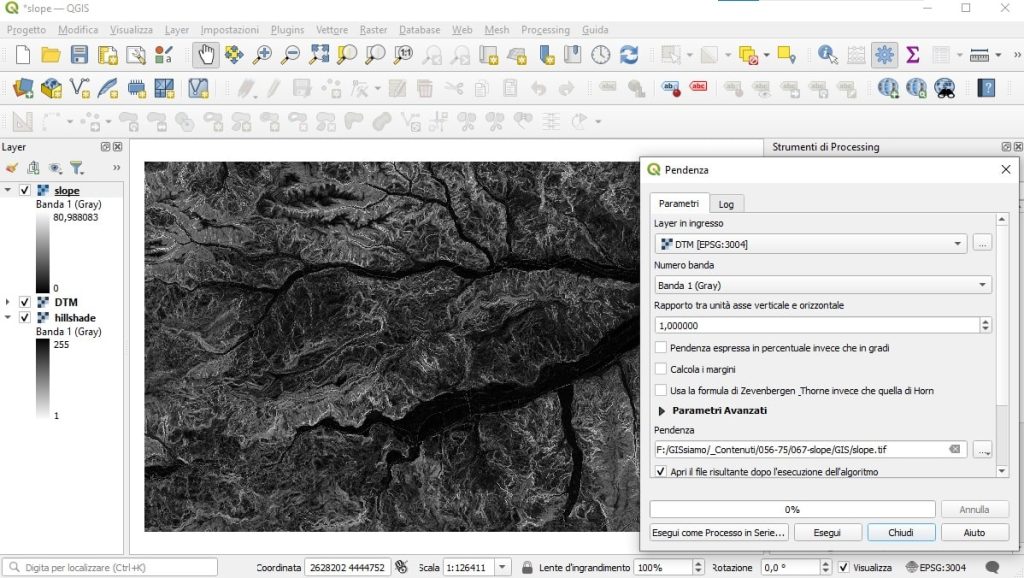
Clicchiamo su Esegui. Et voila, QGIS ha calcolato per noi la pendenza di questa area.

Tips & tricks I

Usi più spesso ArcGIS piuttosto che QGIS e sei curioso di sapere qual è la formula usata in ArcMap per il calcolo della pendenza? ArcMap us:

• La formula di Horne per il calcolo delle pendenze.
• La formula di Zevenbergen-Thorne per il calcolo della curvature.

Tips & tricks II

Ti interessa un ulteriore algoritmo per il calcolo delle pendenze che non usi né la formula di Horn, né quella di Zevenbergen-Thorne? Sempre nel pannello degli strumenti di processing puoi trovare, tra gli strumenti presi dalla libreria di SAGA, nel gruppo Terrain Analyisis-Morphometry, la tool Slope, Aspect, Curvature. Qui troverai ben 8 algoritmi diversi per il calcolo della slope.

Bene, questo post è finito. Se ti è piaciuto condividilo! Hai dubbi o suggerimenti? Lascia pure un commento.

Puoi vedere anche il nostro video su YouTube “La pendenza in QGIS. La guida definitiva” e iscriverti al nostro canale.

Ciaooo

Per approfondire:

L’articolo a questo link fa il confronto tra diversi algoritmi ed è in italiano: http://www.geolab.polimi.it/wp-content/uploads/2020/03/rcsc.pdf

Il paper di Horn: Horn, B.K.P., 1981. Hill shading and the Reflectance Map. Proceedings of the IEEE, 69 (1), 14-47

Il paper di Zevenbergen-Thorne: Zevenbergen, L.W., and C.R. Thorne, 1987. Quantitative analysis of the land surface topography. Earth Surf. Proc. And Landf., 12, 47-56.

Pendenza, slope, terrain analysis, DTM, tutorial passo passo,  tutorial QGIS italiano, GISsiamo,